Predictive Control Methods
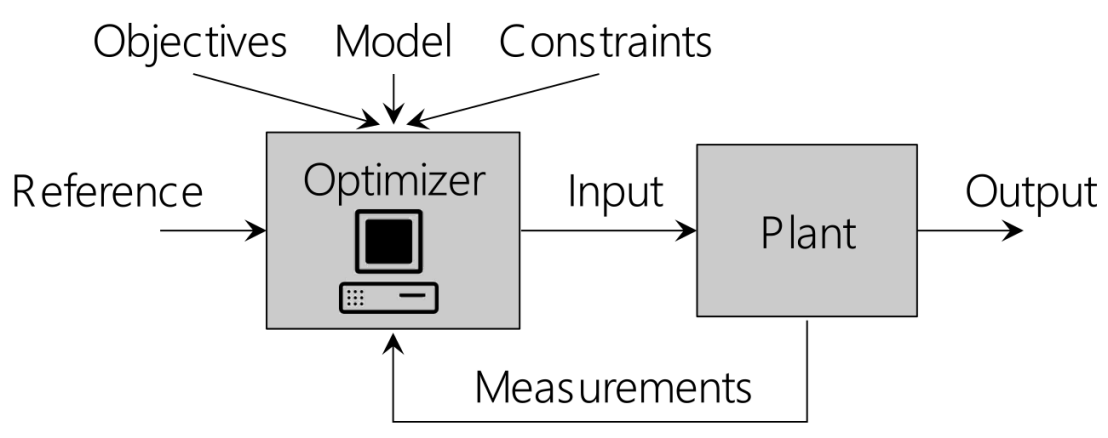
Predictive control methods use finite-horizon model-based predictions to compute an optimal control input. In particular, the minimizing input is computed based on an optimization problem, such that some user-specified cost function is minimized while satisfaction of safety-critical constraints is ensured. Model predictive control (MPC) is an optimization-based control method that generates feedback by repeatedly solving such predictive control problems and applying the initial part of the resulting optimal input sequence.
We are specifically interested in MPC due to its unique ability to guarantee the satisfaction of safety-critical constraints for general nonlinear systems. Our research focuses on extending this safe-by-design property to consider uncertain systems, to account for limited computational resources, and also transfer this safety property to reinforcement learning algorithms.
Model uncertainty in predictive control
In practice, the model used for predictive control is typically affected by uncertainty and the identified model is potentially biased. Therefore, the model uncertainty needs to be taken into account when designing a predictive control method in order to retain the safe-by-design property of model predictive control (MPC).
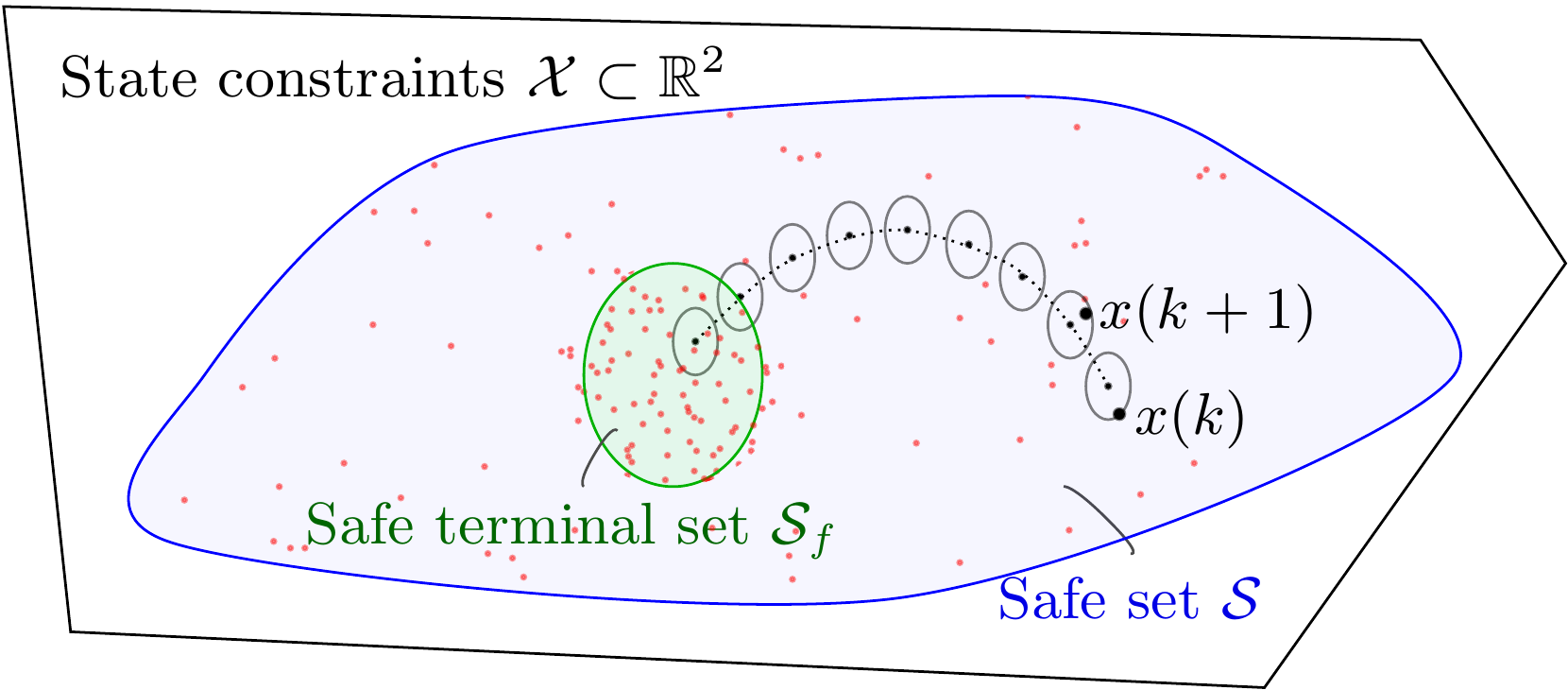
To enforce safety constraint satisfaction despite model uncertainty, we predict an over-approximation of the reachable sets that contain all possible uncertain trajectories. The main goal is the design of computationally tractable predictive control methods with closed-loop safety guarantees. We are mainly interested in the following challenges:
- joint optimization of disturbance feedbacks using a system level approach,
- general nonlinear systems or more general uncertainty characterizations,
- possibly unbounded stochastic disturbances with probabilistic closed-loop guarantees,
- online model updates using adaptation/learning.
Most robust MPC methods are conservative because they fix a pre-stabilizing feedback gain independently of the open-loop plan. This limitation can be addressed by optimizing disturbance feedbacks jointly with the nominal trajectory. This problem can be cast as a System Level Synthesis (SLS) problem where we optimize directly over the closed-loop responses. Besides, sparsity constraints on the controller can be imposed to synthesize a distributed controller by solving a convex optimization problem.
Many industrial applications and theoretical guarantees are tailored to linear systems with bounded additive disturbances. However, a vast majority of systems to be controlled are inherently nonlinear, and better performances could be achieved by operating them where the linearity assumption does not hold. We help push the performance to their physical limit by developing robust MPC methods that leverage general disturbance bounds (e.g., state and input dependent disturbance bounds) and are applicable to general nonlinear systems.
Often, the noise/disturbances can be characterized using a stochastic description (e.g., Gaussian random variables). We study stochastic MPC formulations that utilize such distributional information to ensure a high probability of constraint satisfaction (safety). The fact that arbitrary large unlikely disturbances may occur, makes the design of MPC schemes with guaranteed recursive feasibility and closed-loop properties challenging.
The prediction model often contains parameters that can change during operation (e.g., due to wear) or in general only an inaccurate estimate of the parameters is available. This issue can be addressed by using the collected data to adapt the parameter estimates during runtime. We develop frameworks that incorporate such online model adaptation/learning to improve performance, reduce conservatism, all while retaining the safety properties of MPC.
Selected Publications
L. Hewing, K. P. Wabersich, M. Menner, M. N. Zeilinger. external page Learning-Based Model Predictive Control: Toward Safe Learning in Control. Annual Review of Control, Robotics, and Autonomous Systems, 2020
J. Sieber, S. Bennani, M. N. Zeilinger. A System Level Approach to Tube-based Model Predictive Control. IEEE Control Systems Letters, 2021
J. Sieber, A. Zanelli, S. Bennani, M. N. Zeilinger. external page System Level Disturbance Reachable Sets and their Application to Tube-based MPC. arxiv: 2111.03564, 2022.
L. Hewing, K. P. Wabersich, M. N. Zeilinger. external page Recursively feasible stochastic model predictive control using indirect feedback. Automatica, 2020
L. Hewing, M. N. Zeilinger. Scenario-based Probabilistic Reachable Sets for Recursively Feasible Stochastic Model Predictive Control. IEEE Control System Letters, 2020
L. Hewing, M. N. Zeilinger. external page Performance Analysis of Stochastic Model Predictive Control with Direct and Indirect Feedback. In Proc. 59th IEEE Conference on Decision and Control (CDC), 2020
S. Muntwiler, K. P. Wabersich, L. Hewing, M. N. Zeilinger. external page Data-driven distributed stochastic model predictive control with closed-loop chance constraint satisfaction. In Proc. European Control Conference (ECC), 2021
J. Köhler, K. P. Wabersich, J. Berberich, M. N. Zeilinger. external page State space models vs. multi-step predictors in predictive control: Are state space models complicating safe data-driven designs?. arXiv:2203.15471, 2022.
J. Köhler, M. N. Zeilinger. external page Recursively feasible stochastic predictive control using an interpolating initial state constraint. arXiv:2203.01073, 2022
K. P. Wabersich, M. N. Zeilinger. external page Nonlinear learning‐based model predictive control supporting state and input dependent model uncertainty estimates, International Journal of Robust and Nonlinear Control, 2021
A. Didier, K. P. Wabersich, M. N. Zeilinger. external page Adaptive Model Predictive Safety Certification for Learning-based Control. IEEE Conference on Decision and Control (CDC), 2021
L. Hewing, J., Kabzan, M. N. Zeilinger. Cautious model predictive control using gaussian process regression. IEEE Transactions on Control Systems Technology, 2020
Contact Persons
Johannes Köhler (external page Google Scholar)
Kim Wabersich (external page Google Scholar)
Andrea Zanelli (external page Google Scholar)
Jérôme Sieber (external page Google Scholar)
Antoine Leeman (external page Google Scholar)
Alexandre Didier (external page Google Scholar)
Collaborations & Funding Sources
European Space Agency: Guidance and control of autonomous in-orbit operation based on embedded real-time optimisation - Co-sponsored PhD OSIP (S. Bennani)
European Space Agency: Anytime Control - Embedded Real-Time Optimal Guidance & Control Technologies for Precision Flight & Landing Systems - Co-sponsored PhD OSIP (S. Bennani)
Numerical methods for predictive control
Model predictive control is an advanced optimization-based control strategy that greatly facilitates complex control design tasks involving, e.g., nonlinear and constrained systems, large-scale systems and systems affected by uncertainty. However, its effectiveness and generality comes at the cost of solving an instance of a parametric mathematical program at every sampling time. Especially for systems with fast dynamics or when limited computational resources are available, this poses a challenging task. For this reason, we develop efficient algorithms and software implementations that allow one to speed up the computations and enable applicability of model predictive control to an increasingly large class of systems and control problems.
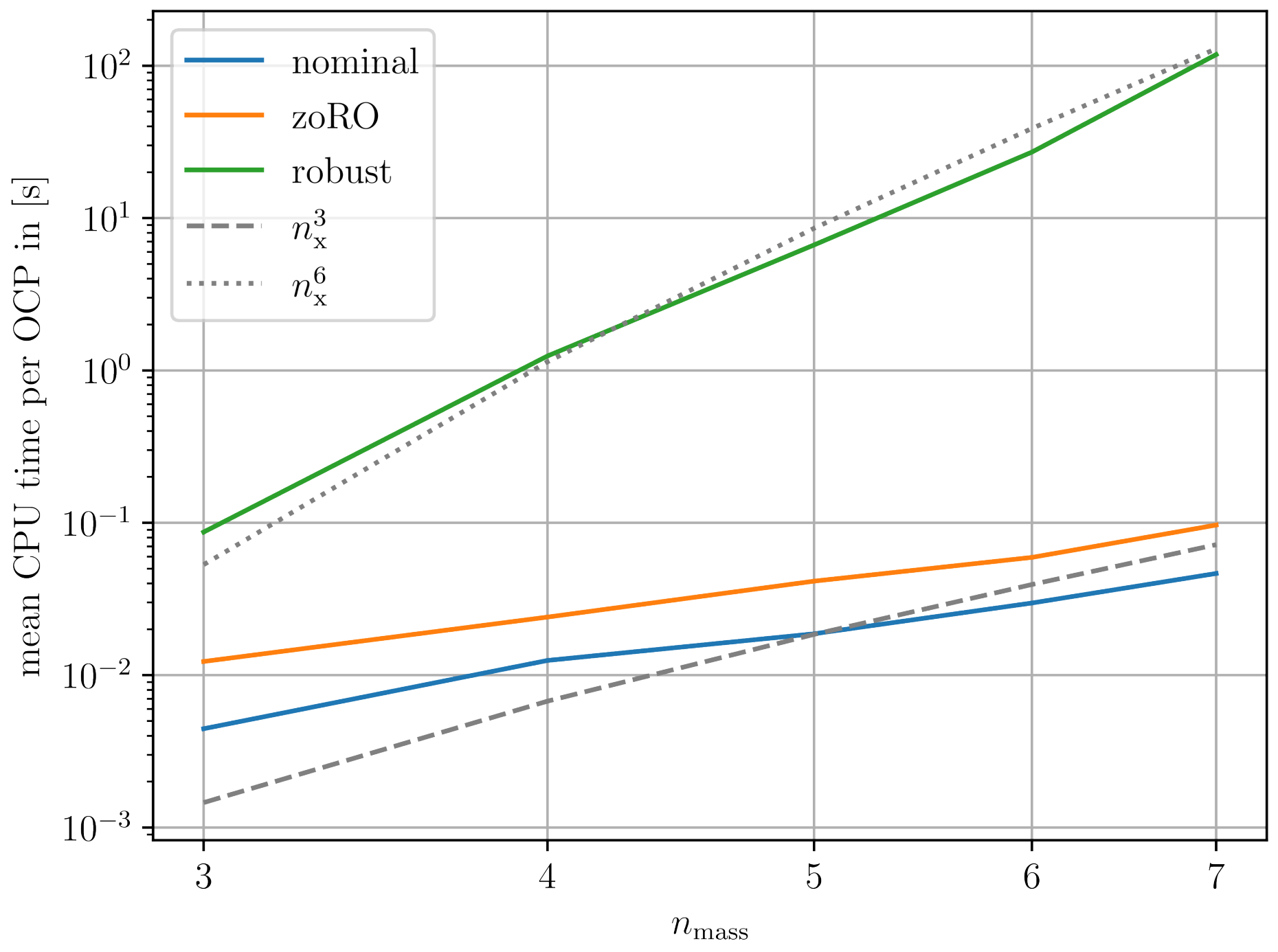
Nonlinear robust and stochastic model predictive control in particular can be computationally heavy as complexity of the algorithms solving the underlying mathematical programs often scales unfavorably with the dimensionality of the state space. We focus part of our research effort on inexact methods that are capable of drastically speeding up the computations by computing suboptimal and yet feasible solutions.
Selected publications and resources
external page Autonomy Talks - A. Zanelli: Efficient inexact numerical methods for nonlinear MPC
In order to guarantee safe operation of the systems to be controlled under stringent computational constraints, we develop methods that are capable of computing approximate and yet feasible solutions at each iteration. In this way, early termination of the solver does only lead to suboptimality, but not to constraint violation.
Selected publications and resources
M. N. Zeilinger, C. N. Jones, M. Morari external page Real-time suboptimal model predictive control using a combination of explicit MPC and online optimization, IEEE Transactions on Automatic Control, 2011.
M. N. Zeilinger, D. M. Raimondo, A. Domahidi, M. Morari, C. N. Jones external page On real-time robust model predictive control, Automatica, 2014.
external page Autonomy Talks - A. Zanelli: Efficient inexact numerical methods for nonlinear MPC
The best way to validate the effectiveness of novel algorithms and software implementations is to deploy them on a physical system and make sure that both computational and control performance meet the requirements of the application chosen. For this reason, we test our algorithms on a range of applications, among which autonomous miniature racing. Due to their fast dynamics, unknown friction forces, and real-time computation requirements, autonomous miniature racing provides a challenging testbed for our algorithms.
Selected publications and resources
external page Autonomy Talks - A. Zanelli: Efficient inexact numerical methods for nonlinear MPC
J. Kabzan, L. Hewing, A. Liniger, and M. N. Zeilinger, external page Learning-Based Model Predictive Control for Autonomous Racing, IEEE Robot. Autom. Lett., 2019.
European Space Agency: Anytime Control - Embedded Real-Time Optimal Guidance & Control Technologies for Precision Flight & Landing Systems - Co-sponsored PhD OSIP (S. Bennani)
European Union’s Horizon 2020 research and innovation programme, Marie Skłodowska-Curie grant agreement No. 953348, external page ELO-X
Predictive safety filter
Predictive safety filters enable the modularization of safety and performance in control design. Applications include the safe application of learning-based controllers, for example, imitation learning for autonomous driving applications, which then allows to safely reproduce a human driver behavior based on available data.
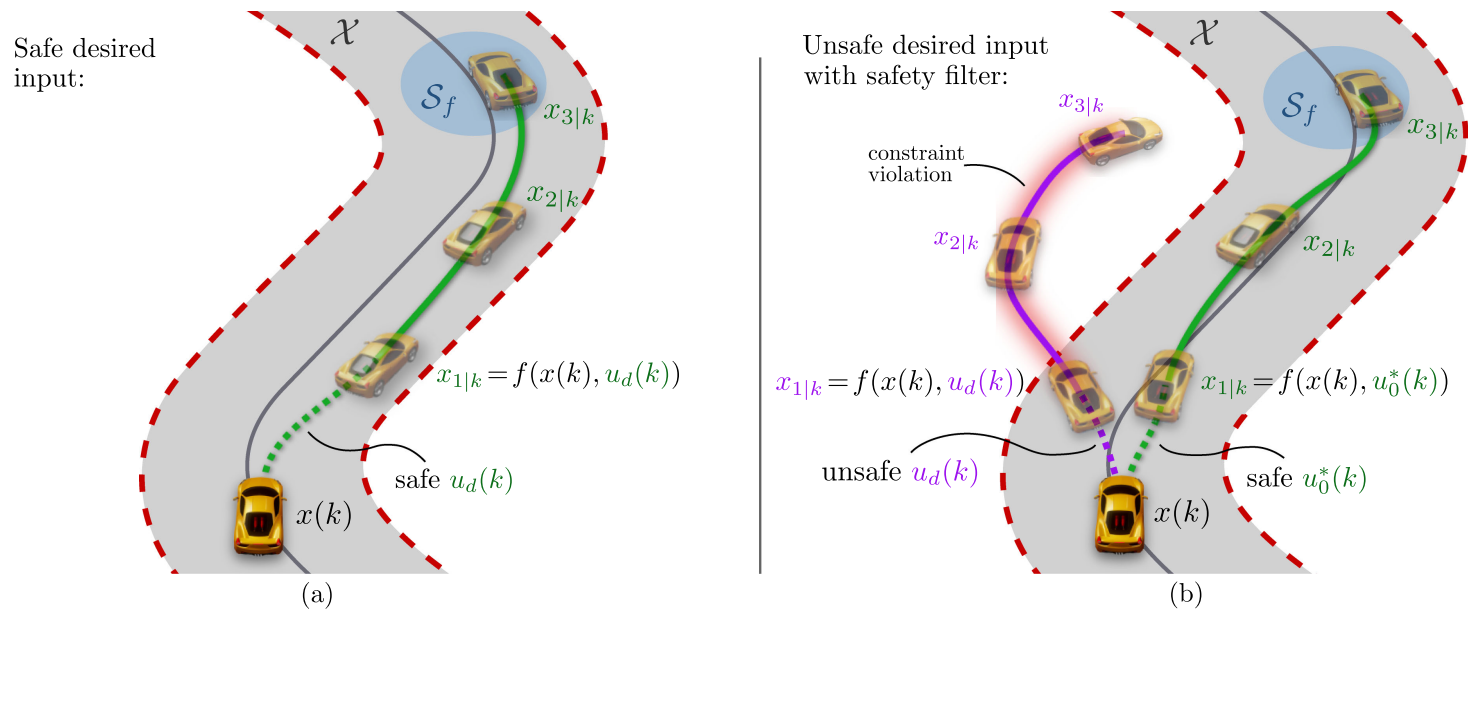
Predictive safety filters allow to enhance existing, potentially unsafe learning-based controllers with safety guarantees. The underlying method is based on model predictive control (MPC) theory and ensures constraint satisfaction through an optimization-based safety mechanism that provides a safe backup control law at all times. To enable the efficient design of the proposed predictive safety filter from system data, our work extends available robustification and stochastic methods from MPC to support diverse system classes through different model assumptions.
Selected Publications
K. P. Wabersich, M. N. Zeilinger. external page A predictive safety filter for learning-based control of constrained nonlinear dynamical systems. Automatica, 2021.
B. Tearle, K. P. Wabersich, A. Carron, M. N. Zeilinger external page A predictive safety filter for learning-based racing control. IEEE Robotics and Automation Letters, 2021.
K. P. Wabersich, L. Hewing, A. Carron, M. N. Zeilinger external page Probabilistic model predictive safety certification for learning-based control. IEEE Transactions on Automatic Control, 2021.
K. P. Wabersich, M. N. Zeilinger. external page Predictive control barrier functions: Enhanced safety mechanisms for learning-based control. arXiv:2105.10241, 2021.