Learning and Estimation
One of the key problems in science and engineering is to provide a quantitative description of the systems under investigation leveraging collected noisy data. Such a description may be intended as a full mathematical model, or as a mechanism to return predictions corresponding to new, unseen, inputs. Our research in learning is targeted both to static and dynamic systems, aiming for strategies that trade off accuracy and computational speed to be used, e.g., in the context of (adaptive) control. In this context, we are also interested in providing algorithms to perform state estimation of dynamical systems from noisy data.
Nonlinear State Estimation
The availability of accurate state estimates is essential for high performance control of safety critical systems. We investigate the design of advanced nonlinear state estimation algorithms for such systems. Our focus is on algorithms with stability properties and quantification of the uncertainty in the state estimate, as well as the use of learning algorithms to adapt the estimators online to unknown system models, or to integrate visual measurement units.
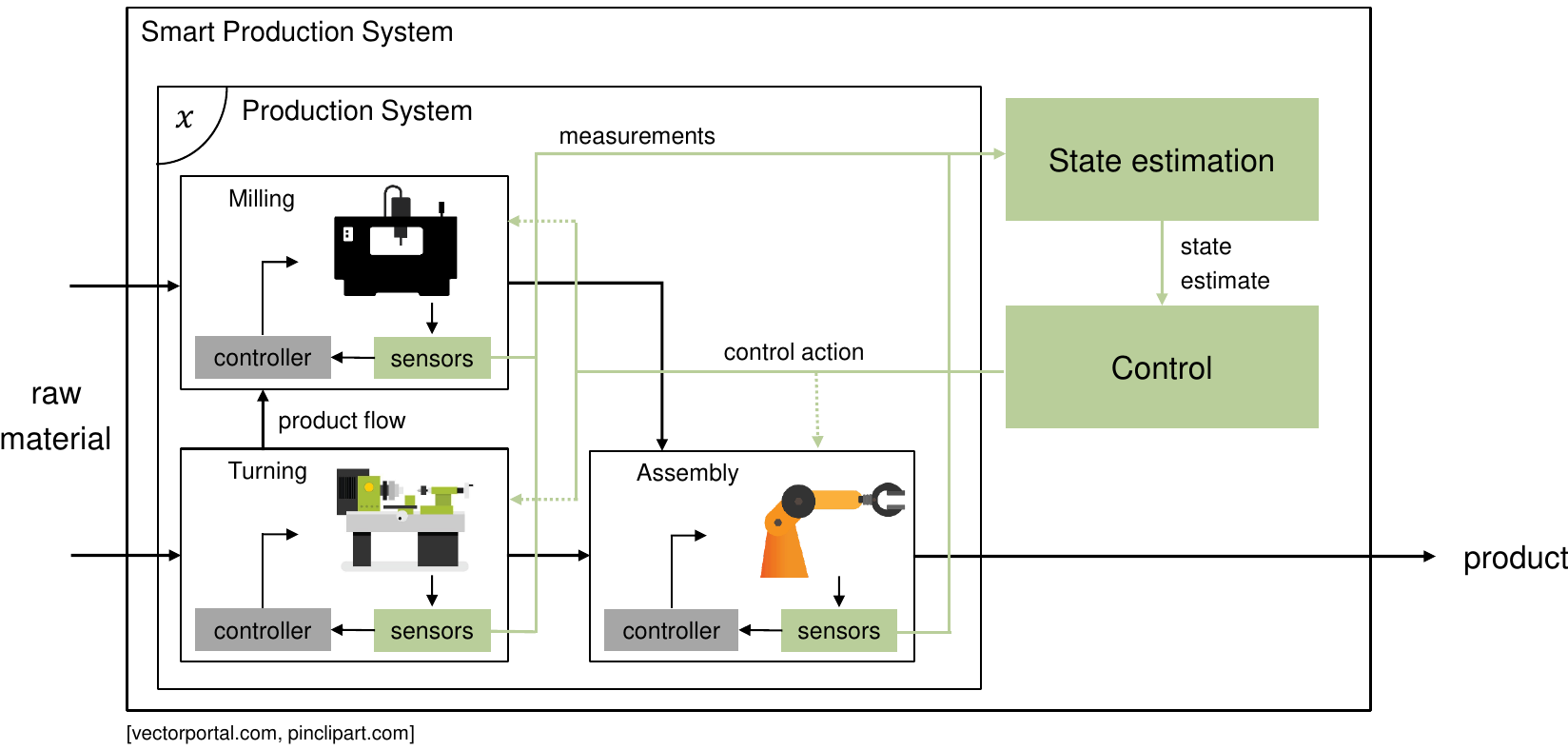
Currently, the main focus within this research project is the development of moving horizon estimation (MHE) algorithms with guaranteed robust stability properties, and the online adaption of MHE estimators to unknown system parameters or underlying changes in the system. Additionally, we investigate the application of extended Kalman filters to estimate system states based on visual sensor measurements. We investigate the application of the developed algorithms in the area of autonomous racing and manufacturing control
Selected Publications
J. D. Schiller*, S. Muntwiler*, J. Köhler, M. N. Zeilinger, M. A. Müller: external page A Lyapunov Function for Robust Stability of Moving Horizon Estimation. (*equal contribution) e-Print arXiv:2202.12744, 2022.
S. Muntwiler, K. P. Wabersich, and M. N. Zeilinger: external page Learning-based Moving Horizon Estimation through Differentiable Convex Optimization Layers. e-Print arXiv:2109.03962, 2021.
Contact Persons
Simon Muntwiler (external page Google Scholar)
Jelena Trisovic (external page Google Scholar)
Collaborations & Funding Sources
The work of Simon Muntwiler is funded by the external page Bosch Research Foundation im Stifterverband.
Jelena Trisovic is an ETH AI Center Doctoral Fellow and co-supvervised by Prof. Melanie Zeilinger and Prof. Fisher Yu from the Visual Intelligence and Systems group.
Multi-task/Meta-Learning for Dynamic Systems
In many applications, data are collected from different, but related, operating conditions. Instead of working on the single data-sets, it is usually beneficial to leverage the underlying relatedness to improve the estimation performance. The goal of this project is to develop methods for such a set-up in view of dynamical systems identification.

The rationale of multi-task learning is to leverage task relatedness to perform simultaneous estimation instead of operating on the single datasets; in the case of meta-learning, the goal is to learn such a prior information from data.
The aim of this project is to develop a rigorous theoretical framework addressing this set-up, bridging machine learning tools with dynamic systems identification. In particular, we focus on the so-called regularized kernel-based methods and their approximations to provide reliable and computationally feasible identification strategies.
Selected Publications
E. Arcari, A. Scampicchio, A. Carron and M. N. Zeilinger. "external page Bayesian multi-task learning using finite-dimensional models: A comparative study," 2021 60th IEEE Conference on Decision and Control (CDC), 2021, pp. 2218-2225, doi: 10.1109/CDC45484.2021.9683483.
Contact Persons
Elena Arcari external page (Google Scholar)
Anna Scampicchio (external page Google Scholar)
Active Learning for Model-based Control
Offline system or reward identification becomes increasingly challenging and time-consuming for complex systems and environments. This problem can be addressed by learning-based control techniques, leading to the well-known exploration-exploitation trade-off. This project aims at providing approximate solutions that offer computationally feasible optimization-based formulations for balancing exploration and exploitation in the context of model-based control, both in the case of unknown dynamics, and in the case of unknown cost functions.
Bayesian MPC considers uncertain system dynamics and reward models and combines cautious model predictive control concepts and posterior sampling techniques to obtain an efficient model-based learning algorithm. The technique provides a Bayesian cumulative regret bound on the performance and on the number of unsafe learning episodes.
Selected Publications
K. P. Wabersich, M. N. Zeilinger. external page Bayesian model predictive control: Efficient model exploration and regret bounds using posterior sampling. Learning for Dynamics and Control 2020.
K. P. Wabersich, M. N. Zeilinger. external page Performance and safety of Bayesian model predictive control: Scalable model-based RL with guarantees. arXiv:2006.03483 2020.
Contact Persons
Stochastic dynamic programming inherently solves the problem of goal-oriented control (dual control) by generating policies that optimally trade-off exploration and exploitation, but is computationally intractable. The proposed method systematically derives from the exact solution an approximate, but tractable, formulation that can be cast within an MPC framework using samples. The optimized control sequence is therefore automaticallly equipped with an active learning component.
Selected Publications
E. Arcari, L. Hewing, M. N. Zeilinger. external page An Approximate Dynamic Programming approach for Dual Stochastic Model Predictive Control. IFAC World Congress 2020.
E. Arcari, L. Hewing, M. Schlichting, M. N. Zeilinger. external page Dual Stochastic MPC for Systems with Parametric and Structural Uncertainty. Learning for Dynamics and Control 2020.
Contact Persons
In a multi-agent coverage control problem, multiple agents are tasked to optimize their position to cover a space as best as they can for some density function. With a limited number of agents, this is an NP-Hard problem. Moreover, in practice, the density function is a-priori unknown and agents are subjected to constraints, which are a-priori unknown as well. A core challenge is to provably navigate safely while maximizing a-priori unknown coverage objective. In this work, we exploit the inherent submodularity of the coverage function and establish novel results about provable convergence to a near-optimal solution while exploring safely with high probability.
Selected Publications
Contact Persons
Manish Prajapat
Collaborations & Funding Sources
Work in collaboration with Prof. Krause's LAS group and the ETH AI center
Dynamic Regret Minimization
Dynamic regret is defined as the difference between the incurred cost of a proposed controller and the cost a non-causal controller, with access to all future disturbances, could have achieved. It can be seen as an alternative control objective to H2- and H∞-control. The dynamic regret optimal controller can be exactly computed and can outperform these classical approaches as it adapts to the measured disturbances. The aim of this research is to synthesize dynamic regret minimizing controllers for systems which are safety-critical and have unknown dynamics.
The controller which optimally solves the dynamic regret problem can be computed in the case of linear dynamics with quadratic cost functions. The disturbance feedback structure of the regret optimal controller allows adaptation to disturbances which a system experiences and therefore allows it to outperform classical H2- and H∞-controllers. Furthermore, the regret optimal controller provides a tight regret bound. This bound allows quantifying the additional incurred regret compared to the optimal non-causal controller and is tight in the sense that a disturbance exists such that this bound is achieved. A novel, optimisation-based synthesis method allows considering structured dynamic regret problems, such as a pointwise in time bounded disturbance, as well as systems which are required to operate within state and input constraints. The synthesis of the dynamic regret problem with pointwise bounded disturbances allows giving regret bounds no worse than solving the problem for bounded disturbance energy and is shown to be suboptimal by at most a constant factor.
Selected Publications
A. Didier, J. Sieber and M. N. Zeilinger: external page A System Level Approach to Regret Optimal Control. arXiv preprint arXiv:2202.13763, 2022.